2020-03-10发表技术27 分钟读完 (大约3998个字)

TreeMap 源码解析

TreeMap 是红黑树实现的键值对容器，本文分析其源码和实现原理。

定义

1
2
3

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

TreeMap 基于红黑树（Red-Black tree）实现。该映射根据其键的自然顺序进行排序，或者根据创建映射时提供的 Comparator 进行排序，具体取决于使用的构造方法。

红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质：

每个节点要么是黑色，要么是红色；
根节点是黑色；
每个叶子节点（NIL）是黑色；
每个红色结点的两个子结点一定都是黑色；
任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

初始化

TreeMap 提供了四个构造方法。

// 比较器
private final Comparator<? super K> comparator;

// 红黑树根节点
private transient Entry<K,V> root = null;

// 集合元素数量
private transient int size = 0;

public TreeMap() {
  	comparator = null;
}

public TreeMap(Comparator<? super K> comparator) {
  	this.comparator = comparator;
}

public TreeMap(Map<? extends K, ? extends V> m) {
  	comparator = null;
  	putAll(m);
}

public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
      buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

可以看出构造方法主要是对comparator进行了初始化，后两个方法将 Map 或 SortedMap 中的数据放入此容器中。

TreeMap 的本质是 **R-B Tree(红黑树)**，它包含几个重要的成员变量：root,size,comparator。

root是红黑树的根节点。它是 Entry 类型，Entry 是红黑数的节点，它包含了红黑数的 6 个基本组成成分：key(键)、value(值)、left(左孩子)、right(右孩子)、parent(父节点)、color(颜色)。Entry 节点根据 key 进行排序，Entry 节点包含的内容为 value。
红黑数排序时，根据 Entry 中的 key 进行排序；Entry 中的 key 比较大小是根据比较器comparator来进行判断的。
size是红黑数中节点的个数。

Entry 结构

TreeMap.Entry 是其节点类

private static final boolean RED   = false;
private static final boolean BLACK = true;

static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    Entry<K,V> left;
    Entry<K,V> right;
    Entry<K,V> parent;
    boolean color = BLACK;

    Entry(K key, V value, Entry<K,V> parent) {
        this.key = key;
        this.value = value;
        this.parent = parent;
    }

    public K getKey() {
        return key;
    }

    public V getValue() {
        return value;
    }

    public V setValue(V value) {
        V oldValue = this.value;
        this.value = value;
        return oldValue;
    }

    public boolean equals(Object o) {
        if (!(o instanceof Map.Entry))
          return false;
        Map.Entry<?,?> e = (Map.Entry<?,?>)o;

        return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
    }

    public int hashCode() {
        int keyHash = (key==null ? 0 : key.hashCode());
        int valueHash = (value==null ? 0 : value.hashCode());
        return keyHash ^ valueHash;
    }

    public String toString() {
        return key + "=" + value;
    }
}

该类定义了其父节点、左右子节点的引用，本身的键值以及颜色，实现了equals和hashCode方法。

常用方法解析

put 方法解析

put方法是 Map 最常用的方法之一，调用该方法可以添加键值对到 Map 中。

public V put(K key, V value) {
    Entry<K,V> t = root;
    if (t == null) {
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    else {
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

该方法可以分为以下几步：

检查根节点root，如果为 null 则初始化并赋值，然后返回；否则继续；
根据comparator或 key 对应类已经实现的Comparable的compareTo方法从root开始向下找到对应的节点位置（如果比较时相等则直接给节点的 value 赋值）；
构造 Entry，并根据比较结果插入到父节点的左或右；
调用fixAfterInsertion方法调整树结构；
size和modCount自增。

以上步骤都非常简单，如果不考虑插入后的调整就是普通的二分查找树了，而红黑树和二分查找树在添加节点的最主要区别就是在fixAfterInsertion方法了。

private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;

    while (x != null && x != root && x.parent.color == RED) {
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    root.color = BLACK;
}

parentOf, leftof, rightOf是根据当前节点找父节点、左子节点和右子节点的方法：

private static <K,V> Entry<K,V> parentOf(Entry<K,V> p) {
    return (p == null ? null: p.parent);
}

private static <K,V> Entry<K,V> leftOf(Entry<K,V> p) {
    return (p == null) ? null: p.left;
}

private static <K,V> Entry<K,V> rightOf(Entry<K,V> p) {
    return (p == null) ? null: p.right;
}

setColor, colorOf是设置和查询节点颜色的方法：

private static <K,V> boolean colorOf(Entry<K,V> p) {
    return (p == null ? BLACK : p.color);
}

private static <K,V> void setColor(Entry<K,V> p, boolean c) {
    if (p != null)
        p.color = c;
}

rotateLeft, rotateRight是左旋和右旋节点的方法：

private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> l = p.left;
        p.left = l.right;
        if (l.right != null) l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else p.parent.left = l;
        l.right = p;
        p.parent = l;
    }
}

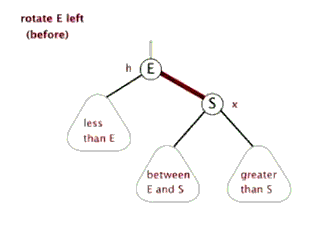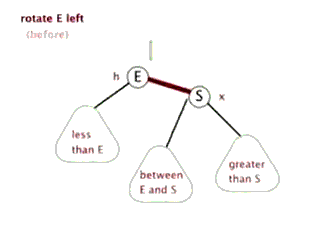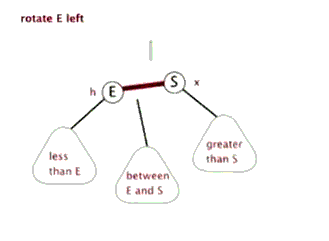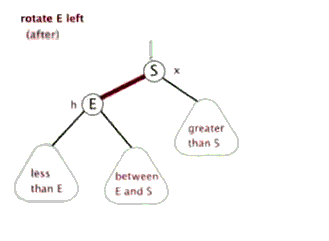
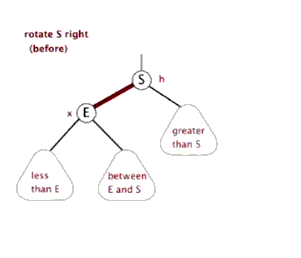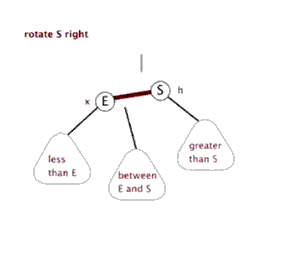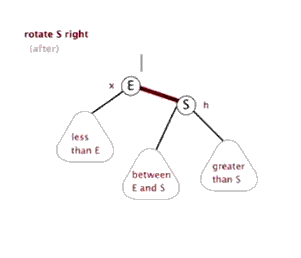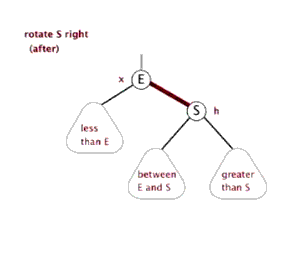
红黑树在插入节点后的调整是变色和旋转，其中旋转又分为左旋和右旋。

左旋和右旋的演示如图：

rotate-left

rotate-right

可以看出旋转虽然调整了树结构，但对每个节点而言其子节点左小右大的规则是不变的。

在红黑树里插入新节点，我们首先将新节点设置为红色，这样可以不违背定义5，减少因为黑高变化而调整的情况。

定义1，2，3都是不会冲突的，那么插入新节点可能导致的就是定义4被打破，因为新添加的节点是红色，而如果其父节点也是红色，就违背了定义4。

为方便分析，我们将祖父节点设为 G，父节点设为 P，叔叔节点设为 U，新插入的节点设为 N

添加新节点时会有以下几种情况，我们拿出 P 是一个左子节点的情况分析：

新增的是根节点，不需要处理；
P 是黑色，不需要处理（新增节点 N 到根节点下也属于此情况）；
P 是红色，需要调整：

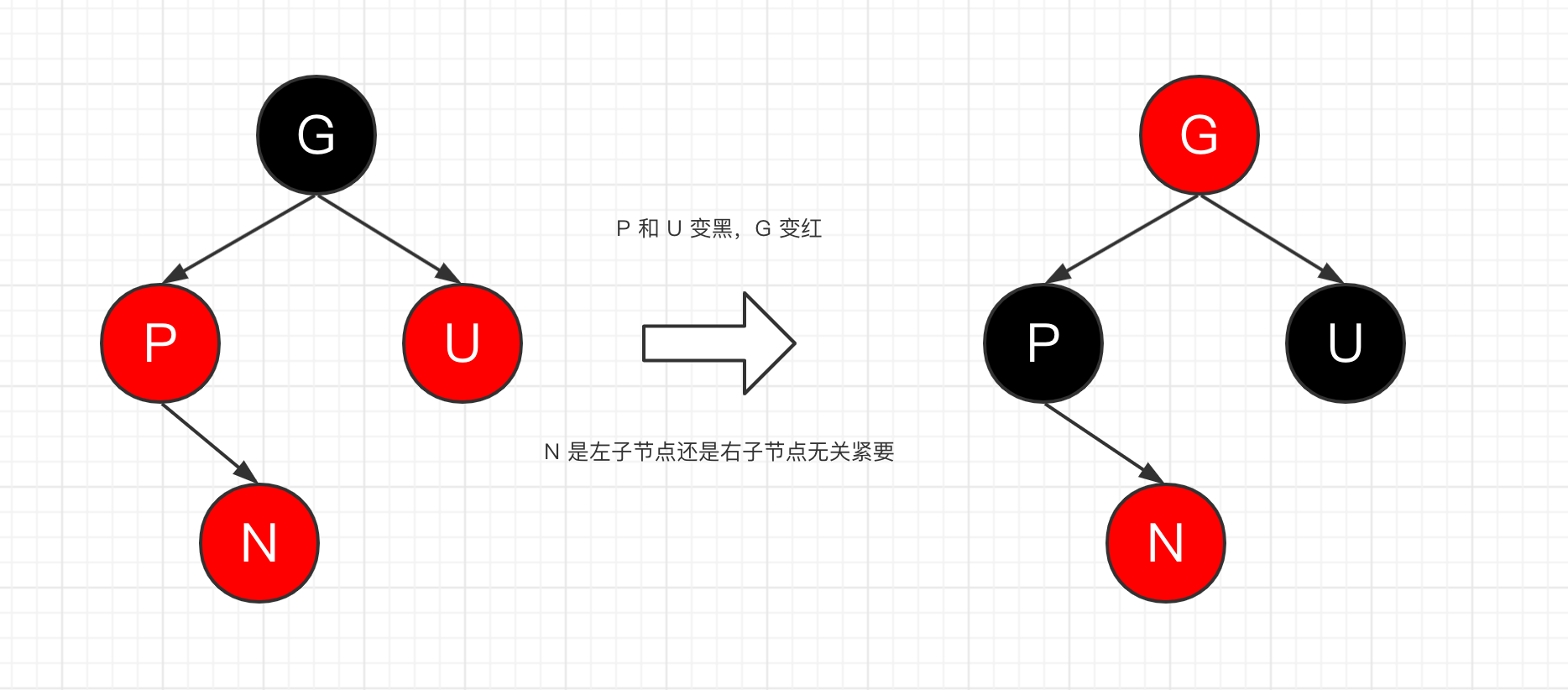
（1）P 和 U 都是红色，此时把 P 和 U 都变黑，然后把 G 变红，再把 G 视作新插入的节点重新调整；如果此时 G 是根节点则变黑即可；

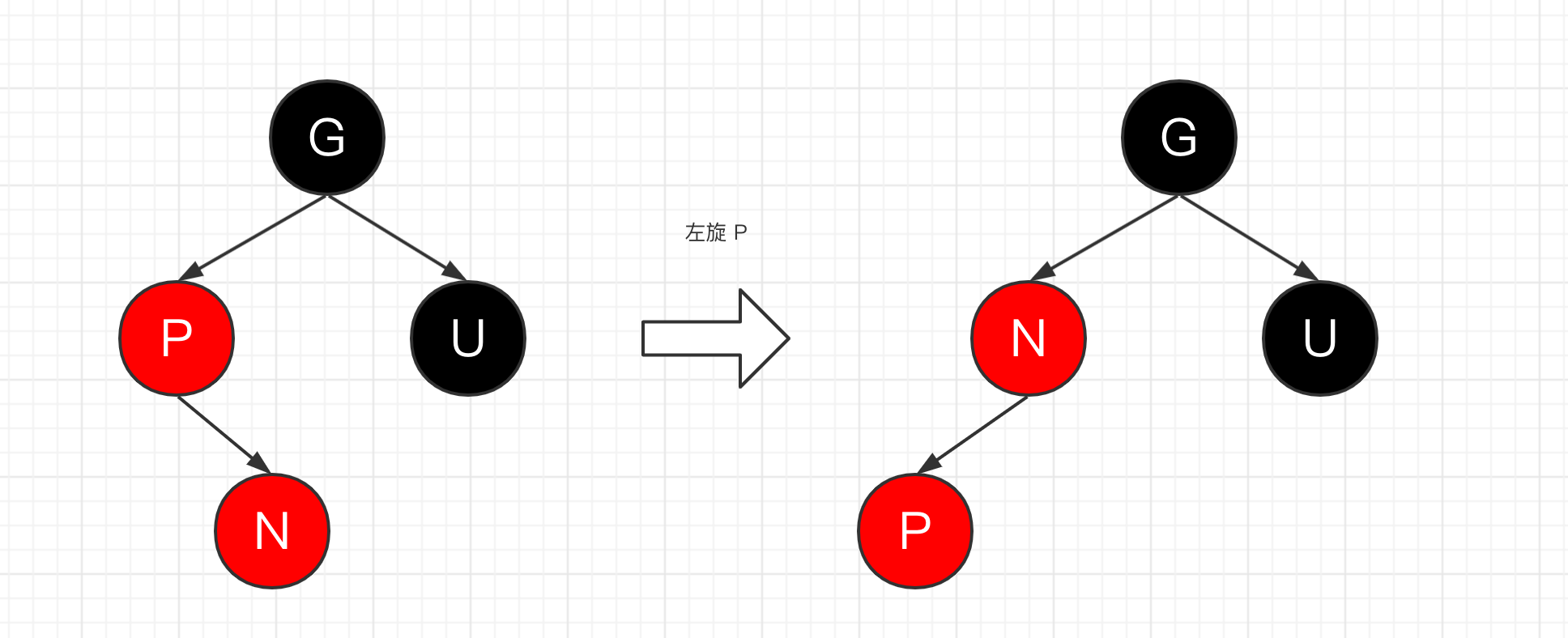
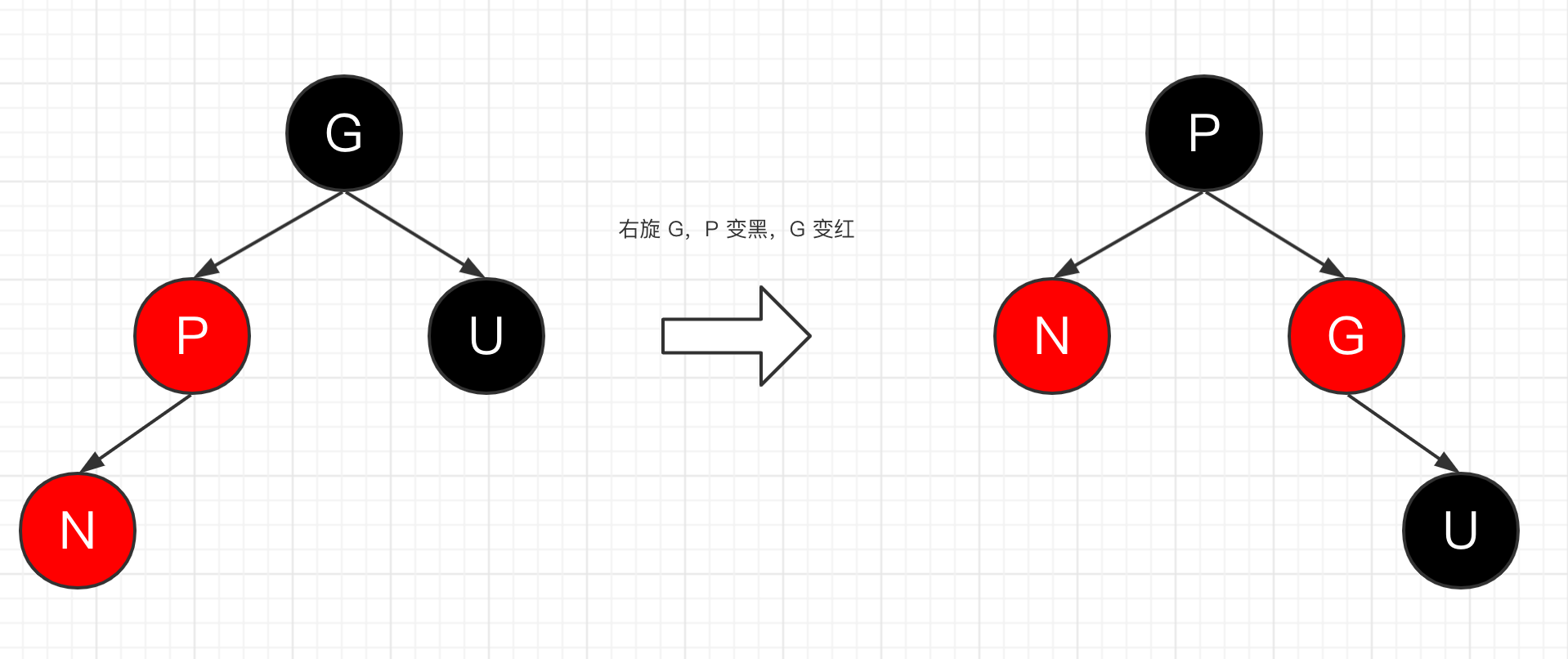
（2）P 红色，U 是黑色，此时若新插入节点是右子节点，P 左旋，变成插入左子节点的情况；如果本身就是左子节点，那么继续将 G 右旋，然后 P 变黑，G 变红即可。

若 P 为右子节点，那么镜像操作即可。

将以上情况实现为代码，就是fixAfterInsertion了。

remove 方法解析

remove方法根据 key 来删除红黑树里的元素。

public V remove(Object key) {
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;

    V oldValue = p.value;
    deleteEntry(p);
    return oldValue;
}

首先调用getEntry获取对应的 Entry，getEntry方法也是查询方法的具体实现，后面再分析。

之后调用deleteEntry方法删除具体的节点。

/**
 * Delete node p, and then rebalance the tree.
 */
private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size--;

    // If strictly internal, copy successor's element to p and then make p
    // point to successor.
    if (p.left != null && p.right != null) {
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    } // p has 2 children

    // Start fixup at replacement node, if it exists.
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);

    if (replacement != null) {
        // Link replacement to parent
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;

        // Null out links so they are OK to use by fixAfterDeletion.
        p.left = p.right = p.parent = null;

        // Fix replacement
        if (p.color == BLACK)
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // return if we are the only node.
        root = null;
    } else { //  No children. Use self as phantom replacement and unlink.
        if (p.color == BLACK)
            fixAfterDeletion(p);

        if (p.parent != null) {
          if (p == p.parent.left)
              p.parent.left = null;
          else if (p == p.parent.right)
              p.parent.right = null;
          p.parent = null;
        }
    }
}

删除节点时，我们依照如下逻辑：

modCount自增，size 自减；
如果被删除的节点没有子节点，直接删除；
如果被删除的节点只有一个子节点，那么删除后用子节点替代本身位置；
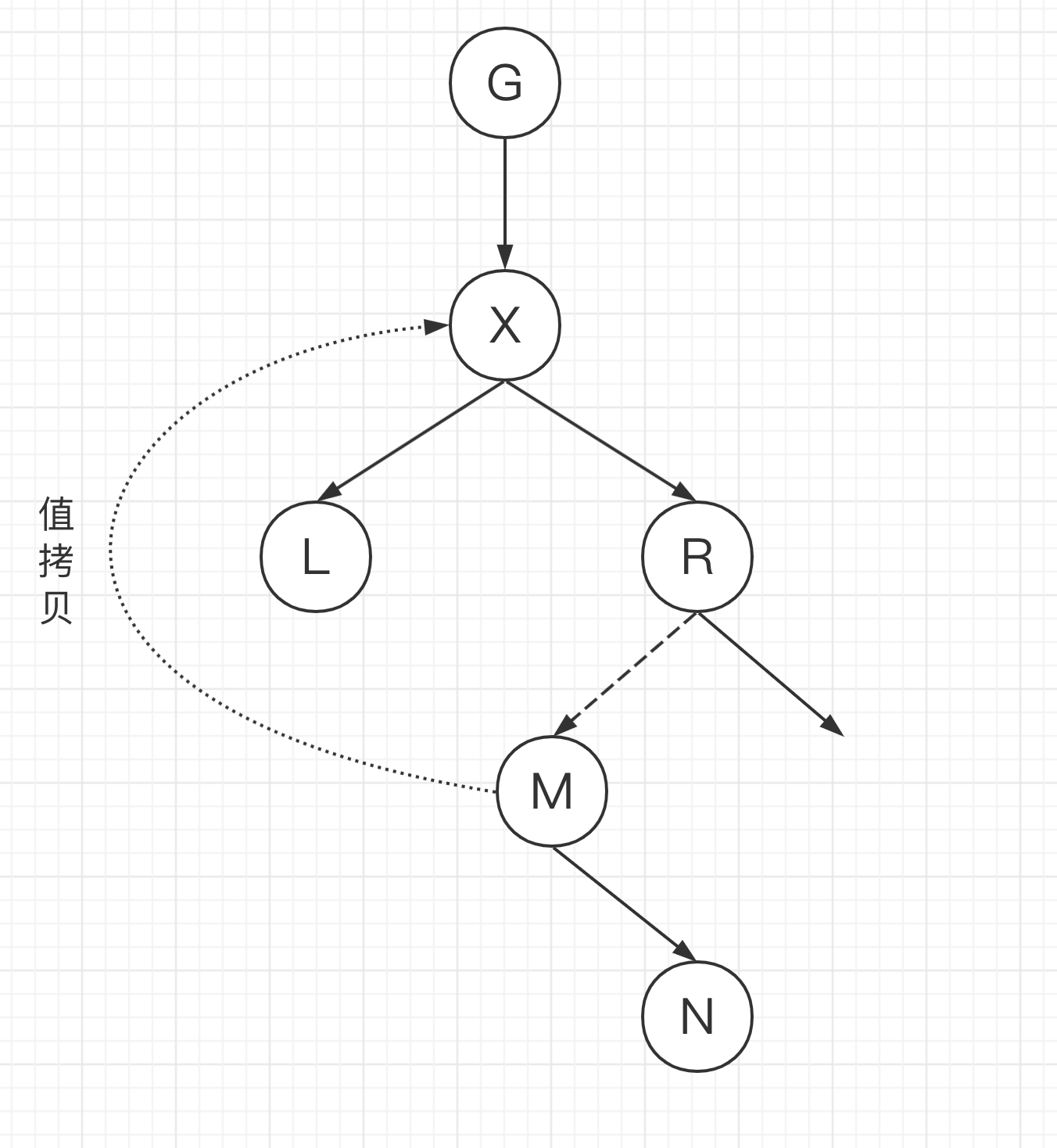
如果被删除的节点有两个子节点，那么找到右子树上的最小值节点，把值赋值给要被删除的节点；然后把右子树上的最小值节点视作要被删除的节点回到2或3处理；
在步骤3和4中，若删除的节点是黑色，需要调用fixAfterDeletion调整树结构。

查看上述步骤，可以发现实质上我们都是删除了只有一个子节点的节点，然后将子节点作为原节点的替代。若被删节点是红色，黑高不变；否则黑高变化需要调整树结构。

private void fixAfterDeletion(TreeMap.Entry<K,V> x) {
    while (x != root && colorOf(x) == BLACK) {
        if (x == leftOf(parentOf(x))) {
            TreeMap.Entry<K,V> sib = rightOf(parentOf(x));

            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);
                setColor(parentOf(x), RED);
                rotateLeft(parentOf(x));
                sib = rightOf(parentOf(x));
            }

            if (colorOf(leftOf(sib))  == BLACK &&
                    colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED);
                x = parentOf(x);
            } else {
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK);
                    setColor(sib, RED);
                    rotateRight(sib);
                    sib = rightOf(parentOf(x));
                }
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK);
                setColor(rightOf(sib), BLACK);
                rotateLeft(parentOf(x));
                x = root;
            }
        } else { // symmetric
            TreeMap.Entry<K,V> sib = leftOf(parentOf(x));

            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);
                setColor(parentOf(x), RED);
                rotateRight(parentOf(x));
                sib = leftOf(parentOf(x));
            }

            if (colorOf(rightOf(sib)) == BLACK &&
                    colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);
                x = parentOf(x);
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);
                    setColor(sib, RED);
                    rotateLeft(sib);
                    sib = leftOf(parentOf(x));
                }
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK);
                setColor(leftOf(sib), BLACK);
                rotateRight(parentOf(x));
                x = root;
            }
        }
    }

    setColor(x, BLACK);
}

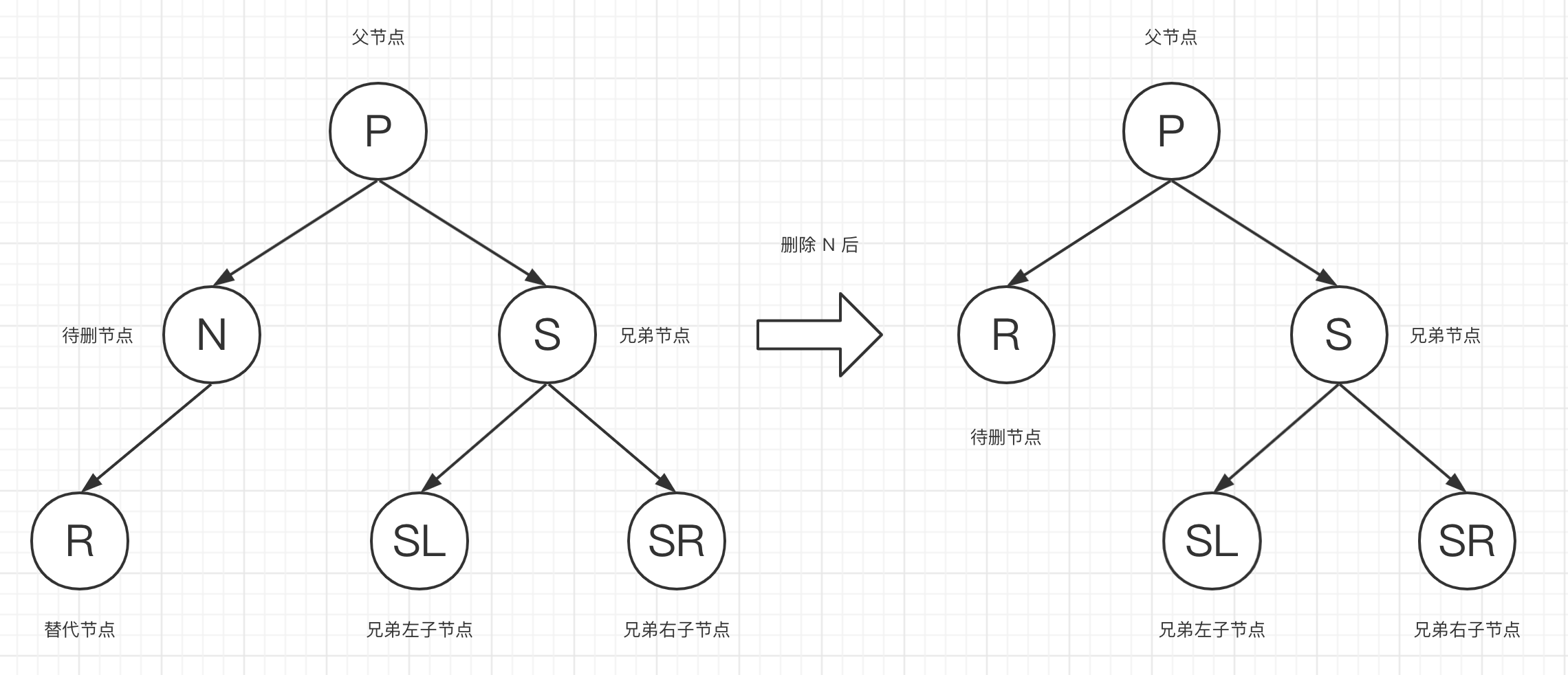
为方便演示，我们进行如下定义：被删节点为 N(Node) ，需要调整的替代节点为 R(Replacement)，其父节点为 P(Parent)，兄弟节点为 S(Sibling)，兄弟节点的子节点分别为 SL 和 SR，图仅演示 N 为左子节点的情况，若为右子节点镜像处理即可（R 是左子还是右子不影响）。

删除名称定义

首先需要调整的情况下，N 一定是黑色的，若 N 是红色黑高是不变的。

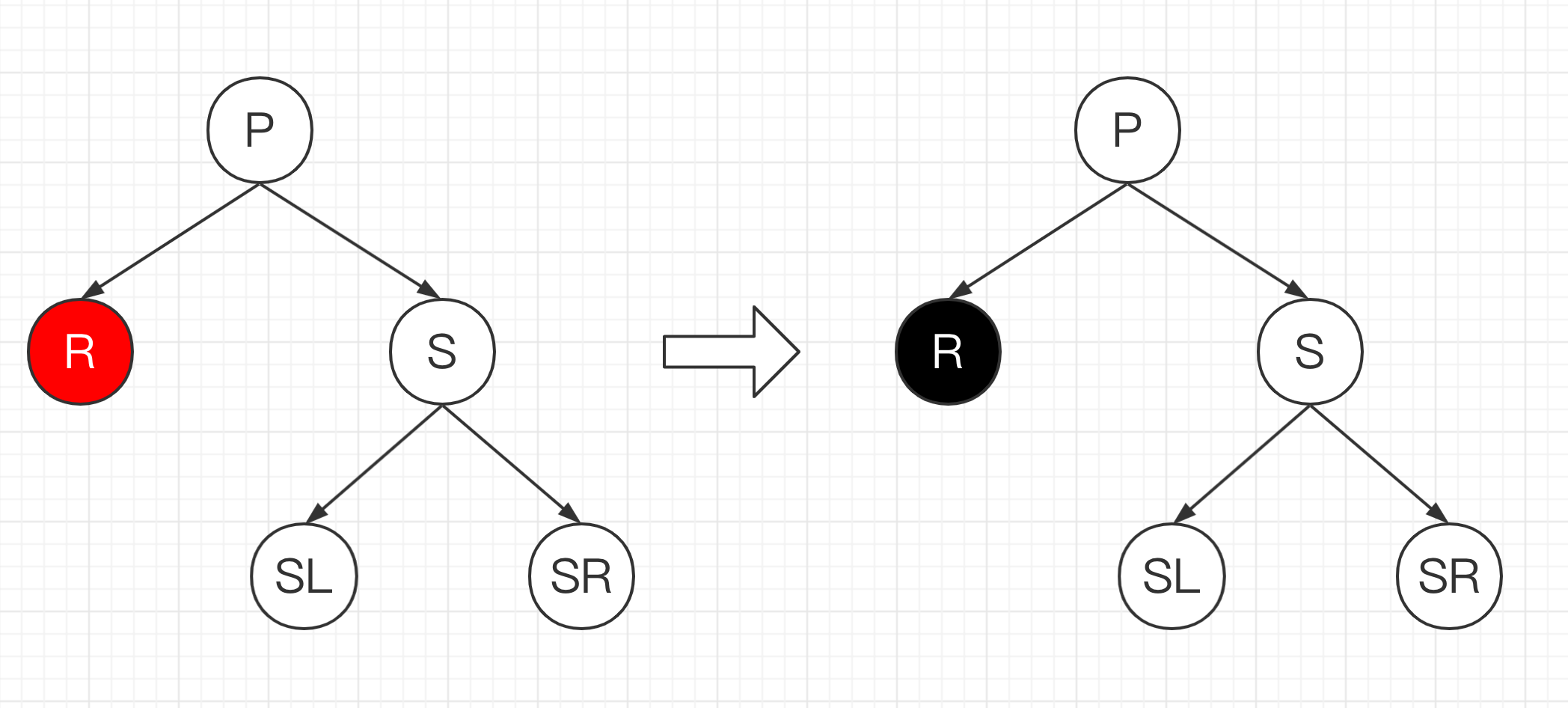
若 R 为红色，将 R 变为黑色即可，此时树结构恢复平衡；
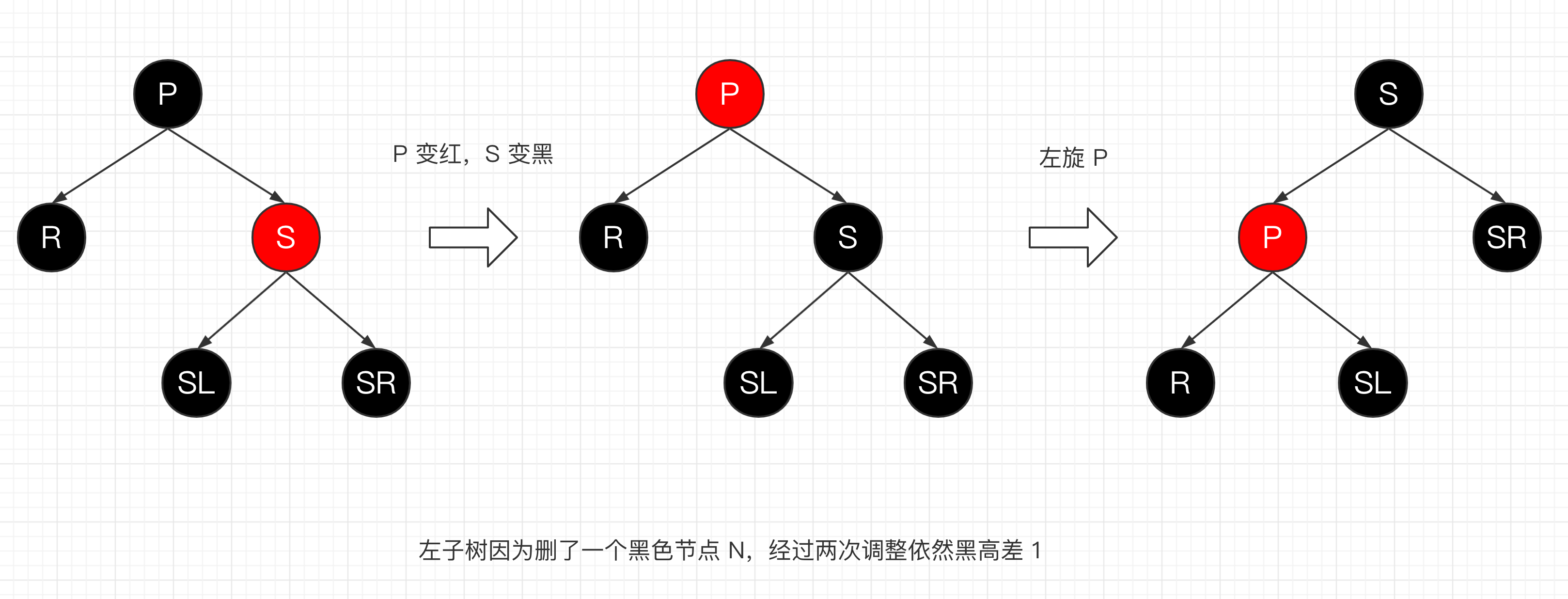
R 为黑色，兄弟节点 S 是红色，此时 S 的父节点 S 和子节点 SL，SR 必然是黑色的；首先将 P 变红，S 变黑，然后左旋 P；之后可以视作 R 的兄弟节点是黑色，父节点是红色的情况进入 5 处理；
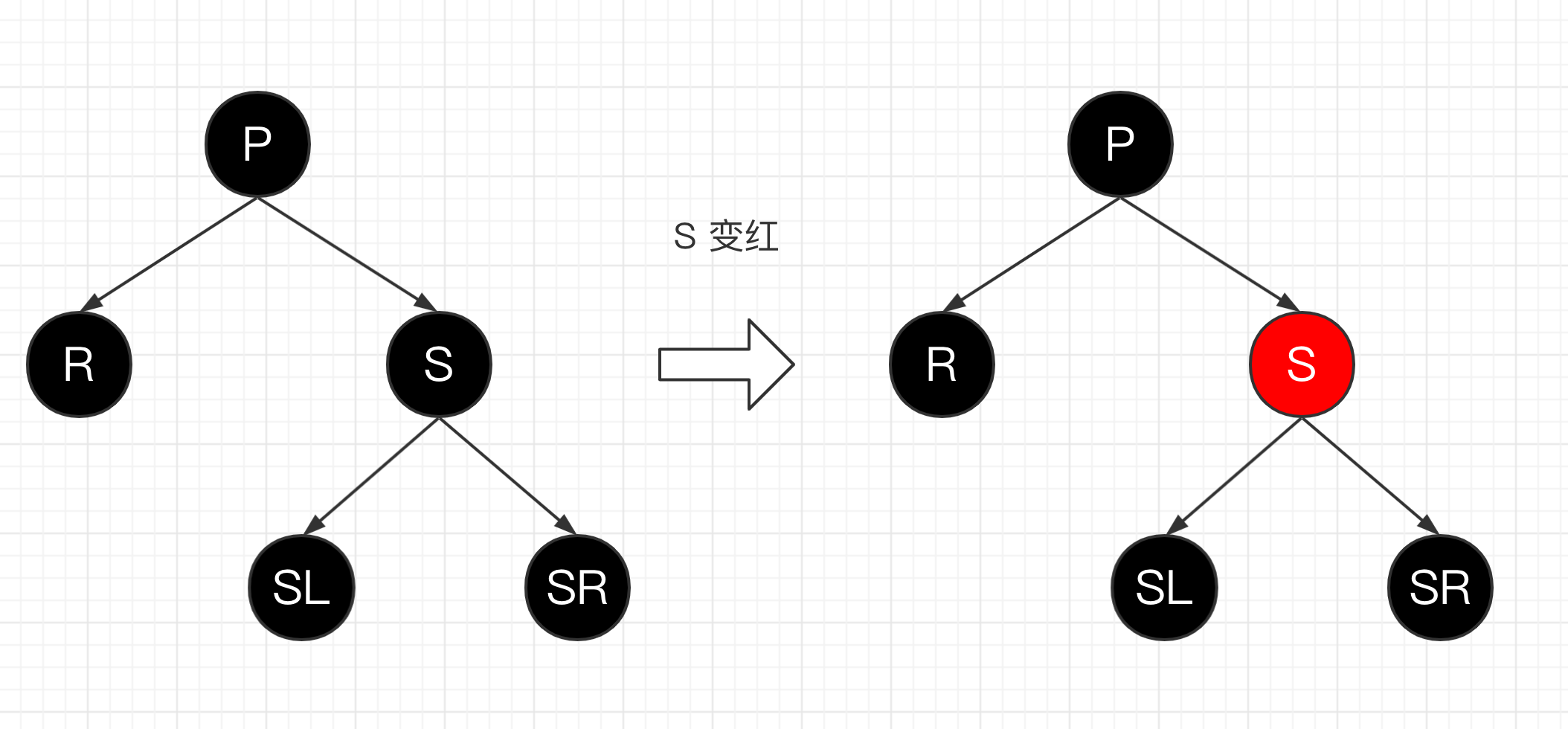
R，P，S，SL 和 SR 都是黑色；我们将 S 变红，此时对 P 的父节点而言 P 子树整体黑高减1，所以需要将 P 整体视作一个替代节点重新调整；
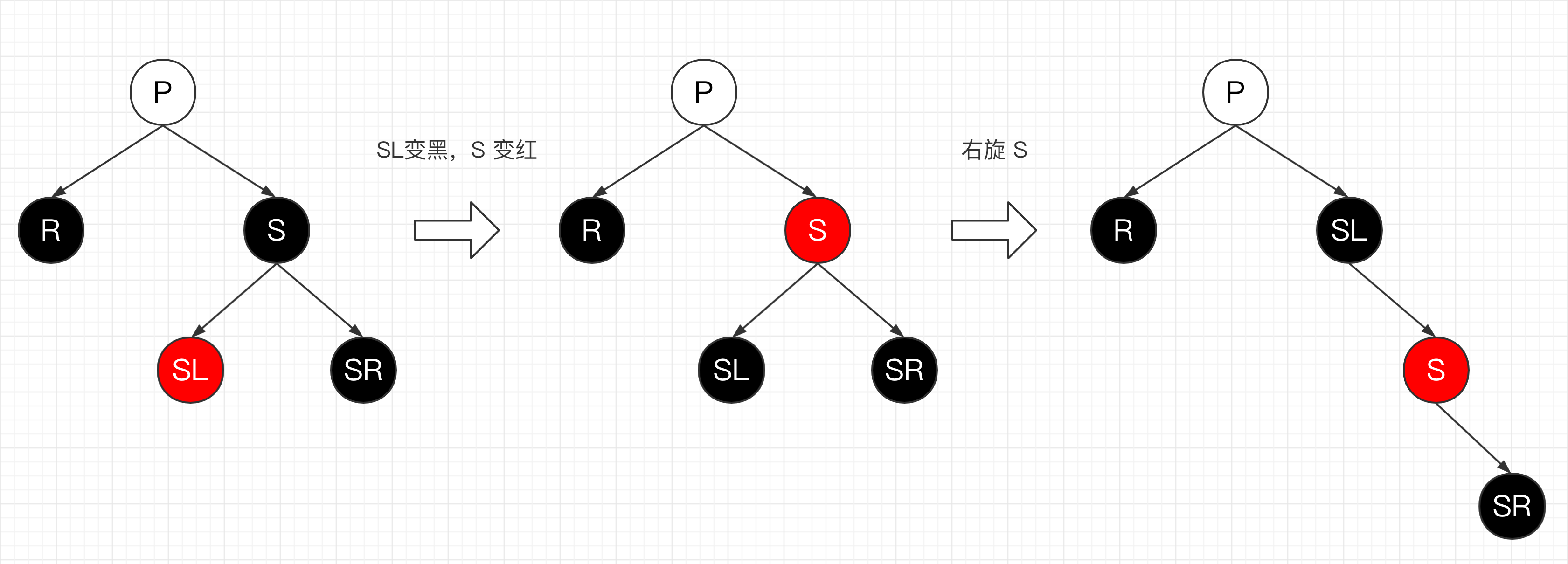
R，S 是黑色，SL 是红色，SR 是黑色；将 SL 变黑，S 变红，再右旋 S；之后我们可以进入 5 处理；
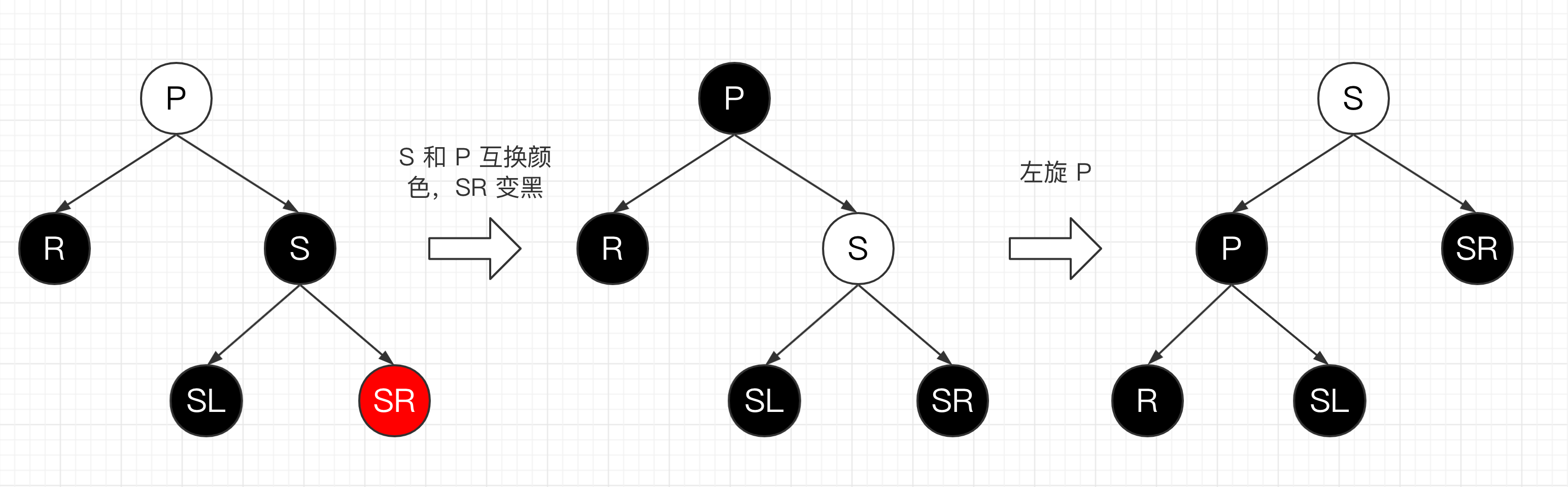
R，S 是黑色，SL 是黑色，SR 是红色；互换 P 和 S 的颜色，SR 变黑，然后左旋 P；无论 P 初始时是什么颜色都能得到一个重新平衡的树。

将以上情况实现为代码，就是fixAfterDeletion了。

get 方法解析

TreeMap 的get方法与二分查找树没有区别，相比起插入和删除较为简单。

public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

final Entry<K,V> getEntry(Object key) {
    // Offload comparator-based version for sake of performance
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
    Comparable<? super K> k = (Comparable<? super K>) key;
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

final Entry<K,V> getEntryUsingComparator(Object key) {
    @SuppressWarnings("unchecked")
    K k = (K) key;
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        Entry<K,V> p = root;
        while (p != null) {
            int cmp = cpr.compare(k, p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
    }
    return null;
}

代码中若 comparator 不为 null，则使用 comparator 进行比较二分查找；否则将 key 强转为 Comparable 进行比较二分查找。

遍历

TreeMap 的遍历可以通过entrySet()方法获取 EntrySet 遍历键值对；或keySet()获取 KeySet 遍历键；抑或values()获取值的集合来对值遍历。

对 EntrySet 的遍历主要是靠其 Iterator 的next,hasNext方法，先看entrySet方法：

public Set<Map.Entry<K,V>> entrySet() {
    EntrySet es = entrySet;
    return (es != null) ? es : (entrySet = new EntrySet());
}

非常简单，若有就返回，没有就构造一个返回。

其iterator方法：

public Iterator<Map.Entry<K,V>> iterator() {
    return new EntryIterator(getFirstEntry());
}

final Entry<K,V> getFirstEntry() {
    Entry<K,V> p = root;
    if (p != null)
        while (p.left != null)
            p = p.left;
    return p;
}

调用getFirstEntry方法获取 TreeMap 中 key 最小的节点，传入 EntryIterator 中初始化。

final class EntryIterator extends PrivateEntryIterator<Map.Entry<K,V>> {
    EntryIterator(Entry<K,V> first) {
        super(first);
    }
    public Map.Entry<K,V> next() {
        return nextEntry();
    }
}

abstract class PrivateEntryIterator<T> implements Iterator<T> {
    Entry<K,V> next;
    Entry<K,V> lastReturned;
    int expectedModCount;

    PrivateEntryIterator(Entry<K,V> first) {
        expectedModCount = modCount;
        lastReturned = null;
        next = first;
    }

    public final boolean hasNext() {
        return next != null;
    }

    final Entry<K,V> nextEntry() {
        Entry<K,V> e = next;
        if (e == null)
            throw new NoSuchElementException();
        if (modCount != expectedModCount)
            throw new ConcurrentModificationException();
        next = successor(e);
        lastReturned = e;
        return e;
    }

    final Entry<K,V> prevEntry() {
        Entry<K,V> e = next;
        if (e == null)
            throw new NoSuchElementException();
        if (modCount != expectedModCount)
            throw new ConcurrentModificationException();
        next = predecessor(e);
        lastReturned = e;
        return e;
    }

    public void remove() {
        if (lastReturned == null)
            throw new IllegalStateException();
        if (modCount != expectedModCount)
            throw new ConcurrentModificationException();
        // deleted entries are replaced by their successors
        if (lastReturned.left != null && lastReturned.right != null)
            next = lastReturned;
        deleteEntry(lastReturned);
        expectedModCount = modCount;
        lastReturned = null;
    }
}

代码非常简单，hasNext方法检查下一个节点是否为 null，next方法调用nextEntry，nextEntry中先进行合法检查，对节点为 null 和遍历过程中被修改的情况进行判断并抛出异常，再调用successor方法查找后继节点并返回。

总结

TreeMap 是红黑树实现的键值对映射，使用红黑树是为了解决二分查找树可能退化为链表造成的查找效率下降，而红黑树是平衡树里调整树结构较少的一种树，达到了维护和查找的一种折中。

红黑树的调整主要依靠的是变色和旋转，在插入新节点或删除一个节点后其规则可能被打破，此时就需要调整树结构。

在分析 TreeMap 源码之前我一直把红黑树看作一只洪水猛兽不愿面对，但对其庖丁解牛一番，并且画图对照源码，发现其实并不难理解。

红黑树是一种经典的数据结构，分析了 TreeMap 的源码之后也增进了对红黑树的理解，棒棒哒。

TreeMap 源码解析

https://loshine.github.io/2020/03/10/tree-map-source-code-analysis/

作者

Loshine

发布于

2020-03-10

更新于

2024-04-01

许可协议

#Java

TreeMap 源码解析

定义

初始化

Entry 结构

常用方法解析

put 方法解析

remove 方法解析

get 方法解析

遍历

总结

作者

发布于

更新于

许可协议

评论

目录

链接

分类

最新文章

归档

标签